Problem: To convert 2.347 tons/acre to SI units
                with 3 significant digits

given
1 acre = 43560 square feet
1 centimeter = 0.3937 inches
1 pound (lb) = 0.4536 kg
1 US ton = 2000 lb
Below, I have shown how I (dp) would do the conversion. It is described in 6 steps.

Step 1. First, I determine the pertinent SI base units:
The SI unit for length is the meter (m) and the derived unit for area is the square meter (m2).

The SI unit of mass is the kilogram (kg).

So we want to convert tons/acre to kg/m2 .
Step 2. I do a calculation to find out how many kilograms are in a U.S. ton: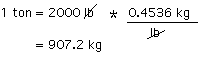

I was not given how many kilograms there are in a ton, but I was given the information that 1 U.S. ton contains 2000 lbs and that 1 lb is equivalent to 0.4536 kg. So I multiplied 2000 lbs by an equivalency factor (0.4536 kg/1 lb). An equivalency factor gives the number of one unit in the numerator, and the equivalent number of another unit in the denominator. Which unit goes in the numerator and which goes in denominator depends on what is being converted to what. In this case I put the lb unit in the denominator because I wanted it to cancel out the lb unit in the expression "2000 lb". If instead of being given 1 pound (lb) = 0.4536 kg, I had been given 1 kg = 2.205 lb, the equivalency factor would have been (1kg/2.205 lb); the result would be the same.
Step 3. I do a calculation to find out how many square meters there are in 1 acre: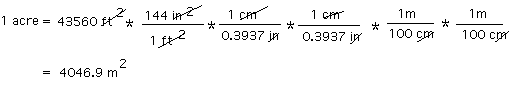
I started with the number of square feet in an acre, which I was given, and multiplied it by a sequence of 'equivalency factors' to get the equivalent in square meters. In the first part of this calculation, I wanted to change square feet to square inches, so I multiplied the number of square feet by (144 in2/1 ft2) so that the ft2units cancel out. (1 square foot = 12 in x 12 in = 144 in 2).

Then I converted square inches to square centimeters using the equivalency factor (1 cm/0.3937 in) squared. (If I had been given 1 inch = 2.54 cm, the equivalency factor would be 2.54 cm/1 inch; the result would be the same.)

Finally I converted square centimeters to square meters by multiplying by (1 m/100 cm) squared.

I cancelled out units as I added equivalency factors. If the calculation was set up correctly, the units that do not cancel out in the end will be the units I want (m2). If it wasn't set up correctly e.g., I multiplied by ft2/in2, rather than in2/ft2, I wouldn't end up with the units I want and I would know that I had made an error.

Once I confirmed that the units were the ones I wanted, I multiplied the numbers with a calculator to give me the numerical part of the answer (4046.9).

Step 4. Now I convert 2.347 tons/acre to units of kg/m2 using the numbers I came up with in (2) and (3) above to make the appropriate equivalency factors: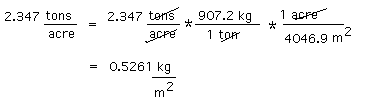
Step 5. I want the number before the units to be between 1 and 999 rather than a smaller or larger number, so I convert kilograms to grams and then round the number off to 3 significant digits.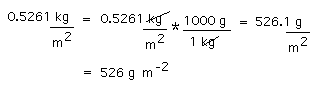
Step 6. I might prefer units that express the yield per square kilometer rather than per square meter; converting the yield from g/m2 to Mg/km2 results in a number between 1 and 999. (Once you get used to the prefixes, it is easy to do such changes in your head).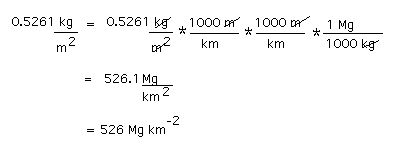
A quicker way of doing it:

I could look on the web for a single factor for converting tons/acre to grams/m2, for example at A DICTIONARY OF UNITS. It turns out they do not provide this factor, however, they do provide factors for converting tons to kilograms (1 ton = 907.2 kg) and acres to square meters (4047 square meters in 1 acre). With those numbers in hand, I could proceed directly to step 4.